What is it about?
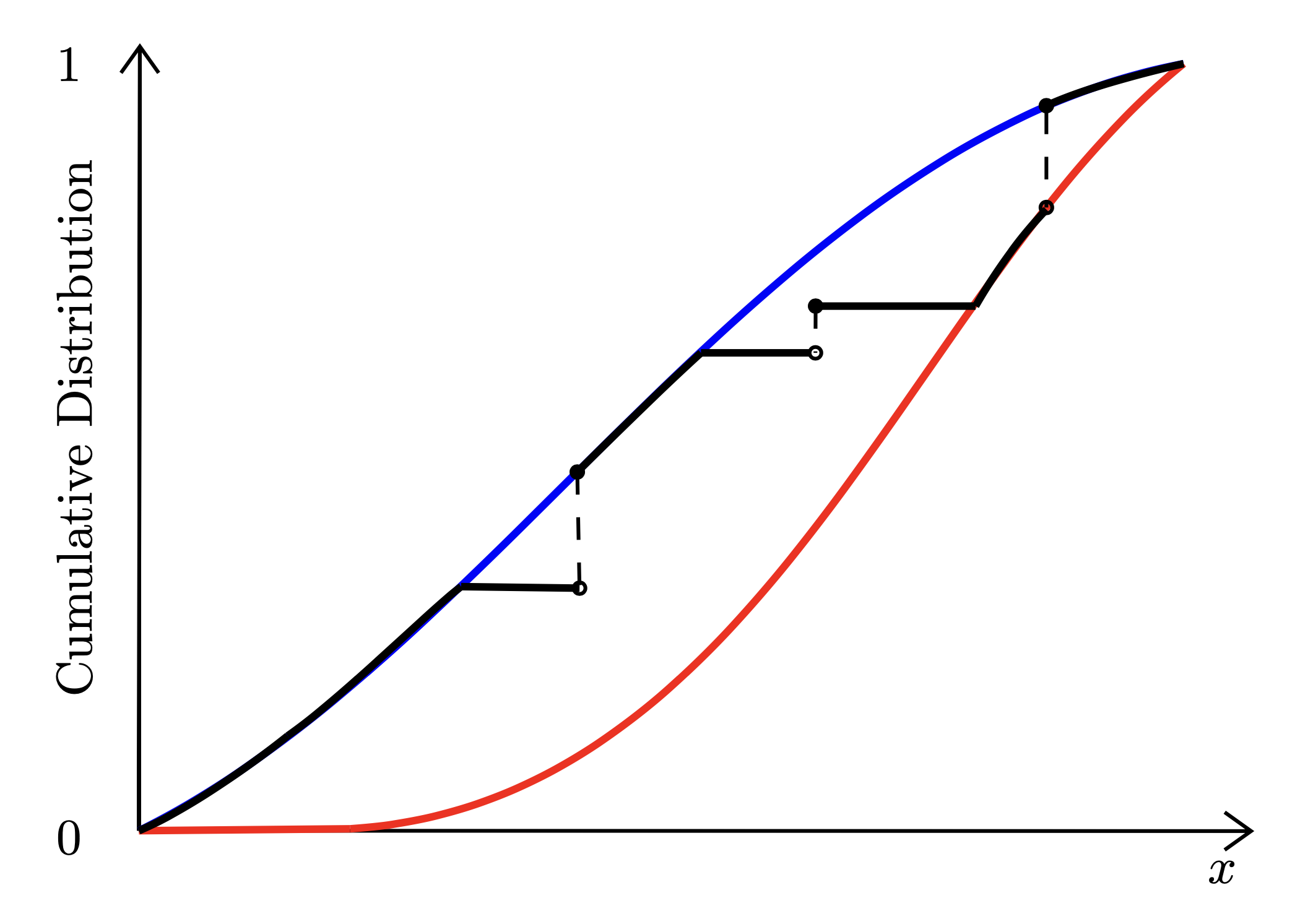
How do electoral districts affect the composition of the Congress? Why are there more than 50% of drivers who think that they are better than the median driver? Is a debt contract more profitable than an equity contract for an entrepreneur to sign with an investor? These seemingly unrelated, and yet canonical, economic questions in fact share a common mathematical structure. By characterizing the extreme points of first-order stochastic dominance intervals, we provide a unifying foundation that connects---and boarden---these questions and more.
Featured Image

Photo by Daniel Peters on Unsplash
Why is it important?
Our characterization help better understanding the mathematical structures of first-order stochastic dominance intervals: distributions that are bounded from above and below in the sense of first-order stochastic dominance. This in turn leads to a characterization of distributions of posterior quantiles, as well as solutions to a wide class of optimization problems that are essential for many economic models.
Perspectives

This article has been a journey. We started with a simple and practical question of what are the possible outcomes (unrestricted) gerrymandering can create. Then we realize that our answer is actually a border characterization of distributions of posterior quantiles, which is a natural analog to the celebrated Strassen's theorem. While writing the paper, we then further realize that the underlying mathematical argument is even more applicable than we had thought, which leads to the characterization of extreme points of FOSD intervals.
Kai Hao Yang
Yale University

Working on this paper was a lesson on searching for patterns that link seemingly unrelated ideas. We had to take concrete topics---like gerrymandering and financial securities---reshape them into their core, abstract forms, and then uncover a common structure that connected them. We had our setbacks, as does all research, but persistence and luck led us to the answer. Undertaking this project with Kai was a deeply gratifying, fruitful, and just plain fun time that I’ll always remember fondly.
Alexander Zentefis
Yale University
Read the Original
This page is a summary of: Extreme Points and First-Order Stochastic Dominance: Theory and Applications, July 2023, ACM (Association for Computing Machinery),
DOI: 10.1145/3580507.3597719.
You can read the full text:
Resources
Contributors
The following have contributed to this page